通信原理

LDPC笔记

LDPC

LDPC 码的基本原理 | 带你读《5G-NR信道编码》之七

LDPC相对于 turbo 码的优势就在于 - 没有低权重码字：码字的hamming距得以增大，获得更小的误码率 - 低复杂度的交互式解码：使用简单的校验 网格

ldpc码可以是系统码也可以是非系统码，关键看你是如何编码的。换句话说，同样的校验矩阵可以用作系统码也可以用作非系统码。这主要根据 G 矩阵的产生方式。

构造 LDPC

LDPC 码的校验阵为稀疏矩阵 A，即 0 的数量远大于 1。

通常用 \((n, t_c, t_r)\) 来描述一个 LDPC 码，其中 \(n\) 为分组长度，\(t_c\) 为各列码重，\(t_r\) 为各行码重，且 \(t_r>t_c\)。

有 \(r=1-\frac{t_c}{t_r}\)

还需检验有效性：令 \(\rho\) 代表 A 中 1 的密度，则可得 \(t_c=\rho(n-k), t_r=\rho n\)，其中 n - k 为 A 的行数，n 为列数（譬如分段长） 故有 \(\frac{t_c}{t_r}=1-\frac{k}{n}\)

overhead（OH，开销）\(=(n-k)/k\)

规则 LDPC 和非规则 LDPC

LDPC 码可以用二分图表示，其中有两种节点：变量节点 和 校验节点

  • 规则 LDPC：每个校验节点连接的变量节点数（3）一致，每个变量节点连接的校验节点数（2）也一致；即：每行有 3 个非零元素，每列有 2 个非零元素
  • 非规则 LDPC：每个节点的自由度可以不一样，但是需要满足：
    • 变量节点自由度\(\lambda(x)=\sum^{d_v}_{i=2}\lambda_ix^{i-1}\)
    • 校验节点自由度\(\rho(x)=\sum^{d_c}_{i=2}\rho_ix^{i-1}\) 系数\(\lambda_i\)和\(\rho_i\)分别表示自由度为\(i\)的从变量节点和校验节点发出的边数所占的比例

然而实际上非规则 LDPC 更灵活，更常用

置信传播

原文链接：https://blog.csdn.net/sinat_38151275/article/details/98102699

译码过程是在变量节点和校验节点之间传递信息。每个变量节点告诉它所连接的校验节点“我认为该变量是什么”，而校验节点告诉它所连接的变量节点“我认为该变量应该是什么”。经过反复的消息传递后，变量节点和校验节点不断改变自己对各个变量是什么的看法，最终能形成一个满足校验方程的码字，这就是译码的结果。如果经过充分的迭代后仍然不能形成一个满足校验方程的码字，则译码器宣布它无法译出这个码字，即译码失败。

Min-Sum

Min：VN到CN，Sum：CN到VN

公式前提：

  • 三比特校验式：\(L_1{\boxplus}L_2{\boxplus}L_3=0{\rightarrow}L_1{\boxplus}L_2=L_3\)
  • 似然比输出：\(L_3=L_1\boxplus{L_2}=\log\frac{P(x_3=+1)}{P(x_3=+1)}=\log\frac{1+e^{L_1}e^{L_2}}{e^{L_1}+e^{L_2}}\)
  • \(\boxplus\)运算：\(L_1\boxplus0=0,L_1\boxplus\pm\infty=L_1\)
  • 最小和近似：\(L_{3}=\operatorname{sgn}\left(L_{1}\right) \cdot \operatorname{sgn}\left(L_{2}\right) \cdot \min \left(\left|L_{1}\right|,\left|L_{2}\right|\right) +\log \left(1+e^{-\left|L_{1}+L_{2}\right|}\right)-\log \left(1+e^{-\left|L_{1}-L_{2}\right|}\right) \\ \approx \operatorname{sgn}\left(L_{1}\right) \cdot \operatorname{sgn}\left(L_{2}\right) \cdot \min \left(\left|L_{1}\right|,\left|L_{2}\right|\right)\)

BP算法校验节点计算： \[ r_{m n}^{k}=\sum_{n^{\prime} \in B(m) \backslash n}^\boxplus q^{k-1} n^{\prime} m \]

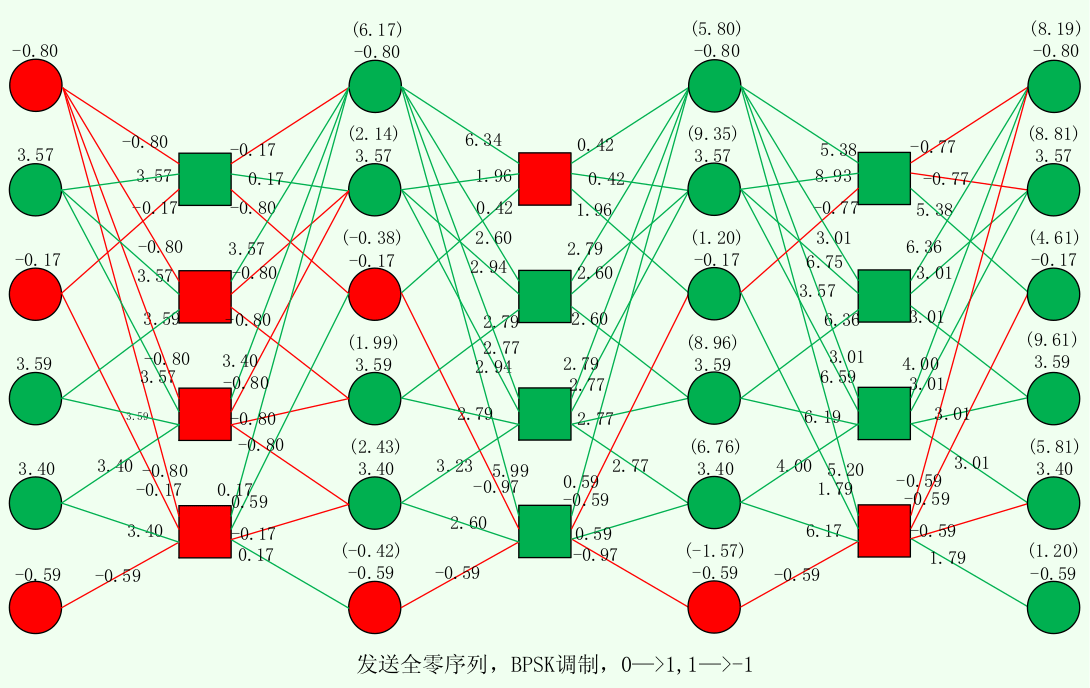
MS算法校验节点计算： - 校验节点对于变量节点i，输出除i以外的其它变量节点的最小和近似。如图中，\(-0.17=sgn(3.57){\cdot}sgn(-0.17){\cdot}min\{|3.57|,|-0.17|\}\) \[ r_{m n, MS}^{k}=\left(\prod_{n^{\prime} \in B(m) \backslash n} \operatorname{sgn}\left(L_{n^{\prime} m}^{k-1}\right)\right) \min _{n^{\prime} \in B(m) \backslash n}\left|q_{n^{\prime} m}^{k-1}\right| \]

变量节点计算： - 变量节点将上一次迭代中从各校验节点接收到的值与自身值相加。如图中，\(6.17=-0.80-0.17+3.57+3.40+0.17\) - 本次迭代中，变量节点向校验节点j输出的值是上式计算出的值减去上次校验节点j向本变量节点输出的值。如图中，\(6.34=6.17-(-0.17)\)

MS算法初始化计算：（与信道噪声方差\(\sigma^2\)无关） \[q^0_{nm}=y_n\]

迭代直到与H相乘为0

下图以发送全零信息为例，绿色为0，红色为1

NMS

Normalized Min-Sum，似乎是直接在 \(L\) 上除以一个大于1的系数即可，而这个系数貌似是定死的。后期演变为ANMS（自动NMS），能够自动调整这个系数。

SPA

（其实应该先讲 SPA 再讲 MS 的）

MS 与 SPA 唯一不同点就在于校验节点的计算。实质上，MS 是 SPA 的简化版，它将 SPA 中的非线性的 \(tanh\)、\(atanh\) 的运算转换为了简单的取最小值。

SPA 的校验节点计算： \[ r_{m n, SPA}^{k}=2\times\operatorname{atanh}\left(\prod_{n^{\prime} \in B(m) \backslash n} \operatorname{tanh}\left(\frac{L_{n^{\prime} m}^{k-1}}{2}\right)\right) \]

复杂度分析

  1. 校验节点：\(O(K\cdot d_c)\)
  2. 变量节点：\(O(N\cdot d_v)\)
  3. 校验式检验：\(O(N\cdot K)\)

若提前终止：\(O(N\cdot K\cdot i)\)

不提前终止：\(O(i\cdot N\cdot d_v)+O(i\cdot K\cdot d_c)+O(N\cdot K)\)

一个校验节点与 \(d_c\) 个变量节点相连，一个变量节点与 \(d_v\) 个校验节点相连

常见常识

  • 编码后的信噪比：\(\frac{E_s}{N_0} = \frac{E_b}{N_0} * rate,rate=\frac{K}{N}\)

NB-LDPC

多元 LDPC 也即是在 \(\mathbf{GF}(q),q=2^{p},p>1\) 的有限域下实现的 LDPC。

GFq

有限域，又叫 伽罗瓦域（Galois Field）

以 \(\mathbf{GF}(4)\) 为例，有限域由 \(0,1,\alpha,\alpha^2\) 组成。在 LDPC 中，通常用 0，1，2，3 这四个十进制数来表示。

有限域的计算法则如下： 1. \(\alpha^2=\alpha+1\) 2. 系数 mod 2

以简单的加法为例： \(1+\alpha^2=1+\alpha+1=\alpha+2=\alpha\)

由此便可得到如下两表（取自维基百科）

 + | 0 1 2 3       ·| 0 1 2 3
 --+--------       --+--------
 0 | 0 1 2 3       0 | 0 0 0 0
 1 | 1 0 3 2       1 | 0 1 2 3
 2 | 2 3 0 1       2 | 0 2 3 1
 3 | 3 2 1 0       3 | 0 3 1 2

所以这些运算常常用查找表来实现，速度快，也很直观。

到底是怎么回事！

参考 伽罗华域(Galois Field，GF，有限域)

好吧，前面的都没讲通，归根结底 \(\mathbf{GF}(q)\) 就是 \(n=\log_2{q}\) 位二进制数，加减法和乘除法都没有进位（也就是模2）。 遇到结果溢出时，就用 本原多项式 把它化归到 n 位内，形成健全的有限域。

那么什么是本原多项式呢？本原多项式可以理解为模2下的素多项式，即： 1. 不能因式分解

列表参考百度百科列出的如下图片：

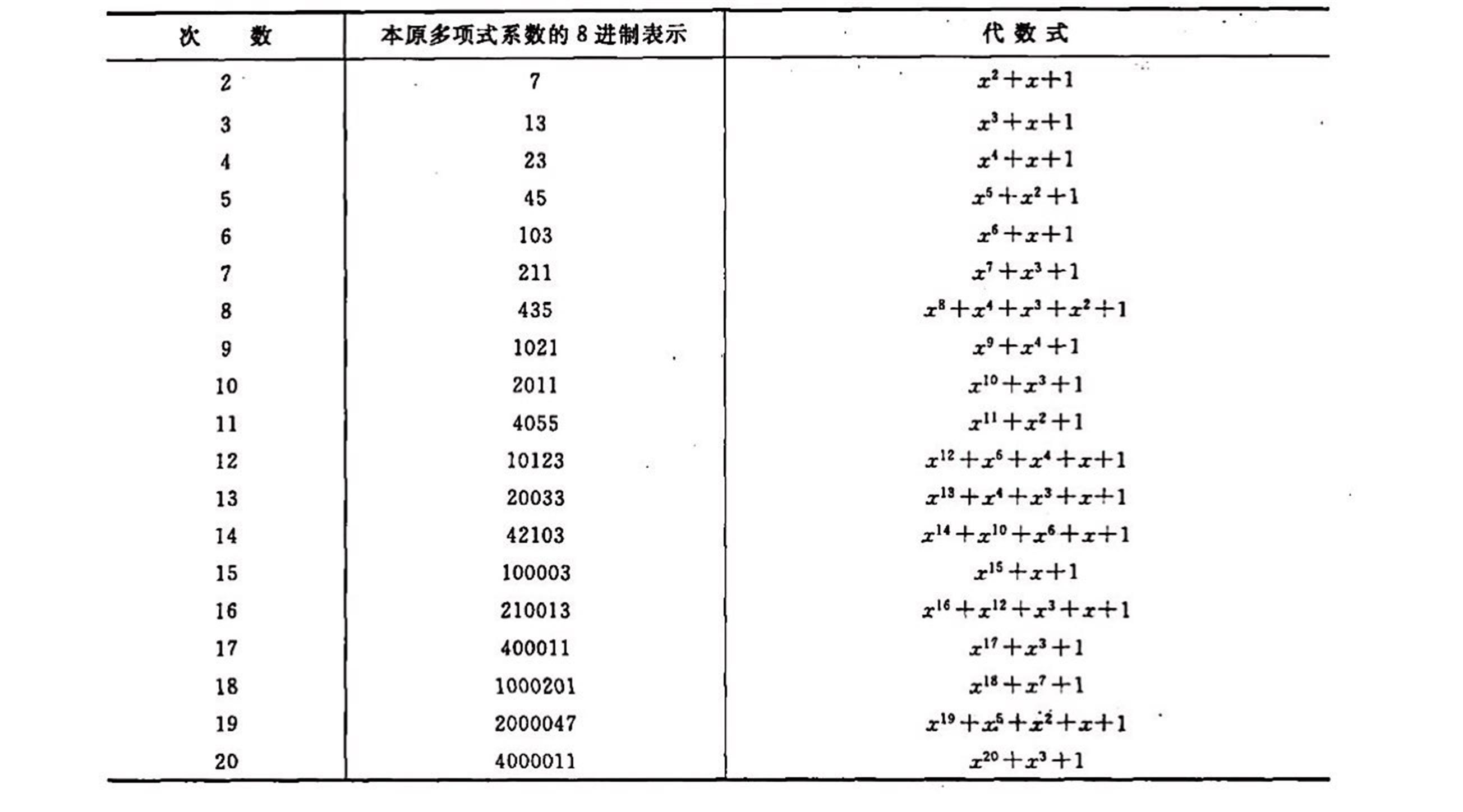
重新回到前面 \(\mathbf{GF}(4)\) 的例子中。 显然，0 = 00, 1 = 01, 2 = 10, 3 = 11，那么，1 + 3 = 01 + 11 = 10 = 2 就理解得通了（不就是直接异或吗喂喂！）； 而减法其实就是加法，因为异或本身就是它自己的逆运算； 再看乘法，2 * 3 = 10 * 11 = 100 + 10 = 11 + 10 = 01 = 1，其中 100 = 11 是根据本原多项式 \(x^3 + x + 1\) 得到的。

为什么我看到的和你说的不一样！

因为实际应用的时候，具体一个十进制数究竟代表哪个多元域的数，有不同的实现方式。

一种方法是 十进制数 \(d\) 代表 \(\alpha^{d-1}\)，\(d=0\) 时代表 \(0\)。这种方法被称为 Power 表示，常在论文中使用。 而还有一种所谓 Vector 表示，也叫 多项式 表示，经常在以 MATLAB 为主的代码实现中使用。这种方法以下图中第三栏中向量的最左为低位，最右为高位，所以 \(\alpha^9=10\) 上一节中由于使用的是 \(\mathbf{GF}(4)\)，两种方法是一致的。

  • Power 表示的加法需要查表，或者转换到 Vector 后异或；而乘法则直接相加
  • Vector 表示的加法直接异或，乘法则同样用查表或者转换到 Power 后相加

有限域带来的麻烦

引入有限域后，许多原本理所应当的操作变得不直观起来。以下会按照 编码-调制解调-解码 来一一观察。

编码： 改用有限域后，由于生成矩阵一般都使用有限域表示，所以信息序列也需要用有限域表示。至于二进制和有限域之间如何转换，只要前后一致即可。

调制解调： 一般使用高阶调制，即一个有限域符号与调制的一个星座点对应，这样性能最好；而如果仍使用 BPSK 等二元调制，则需要将码字转回二元进行调制。

解码 解码时，若使用的二元调制，就要先算出各比特的 LLR，再合成有限域符号的 LLR。而高阶调制则可以直接生成符号 LLR。

\[LLR(b)=\log\frac{Pr(b=0|r=(x,y))}{Pr(b=1|r=(x,y))}\]

AWGN 下的 LLR 计算可以参考 Matlab 文档

QSPA

QSPA，顾名思义，多元下的 SPA。

本质上与 SPA 完全一直，区别在于 LLR 有 Q 个。也就是说， 1. 先前校验节点到变量节点相连的边上只传递一个值，现在则要传递 Q 个，每个对应一个 GF 2. 从变量节点到校验节点也是如此 3. 初始化时，正如上文中 解码 部分所言，也须用 Q 个有限域符号的 LLR 初始化 4. 每次迭代结束后，从变量节点获取值时，选取 Q 个值中最大的那个所对应的 GF 符号，作为该节点的结果，来进行校验

EMS

Extended Min-Sum：使用了配置集的最小和算法。配置集本质就是用于减少搜索范围，即 每个变量节点只有最大的（最可信的） \(n_{max}\) 个值可选，而非 GF 个

第一步，将各校验节点的各多元域符号值（共 \(m\times{GF}\) 个）初始化为 0，变量节点的各符号值（共 \(n\times{GF}\) 个）初始化为各符号的 LLR。

第二步，开始迭代： 1. 遍历各个校验节点 1. 遍历校验节点相连的各变量节点 - 对于各多元域符号（共 \(GF\) 个），计算 遍历到的变量节点 减去 上次本校验节点向该变量节点输出的值（与 B-LDPC 一致） 2. 再次遍历校验节点相连的各变量节点（不含要输出到的变量节点） - 选出上一步中该变量节点得到的值（\(GF\) 个）中 最大的 \(n_{max}\) 个 中的一个 - 将这些值对应的多元域符号 与对应的校验向量相乘，得到要输出的变量节点的多元域符号（这样使得这组变量节点的符号一定满足校验） 3. 根据上一步中选中的各变量节点的多元域符号得到变量节点所对应的值，将其求和 4. 对于当前的变量节点的各个符号，取这一符号满足的所有配置集产生的和中最小的，将其作为输出

下图为一个校验节点中，计算向变量节点 5 输出的值 时的情况。

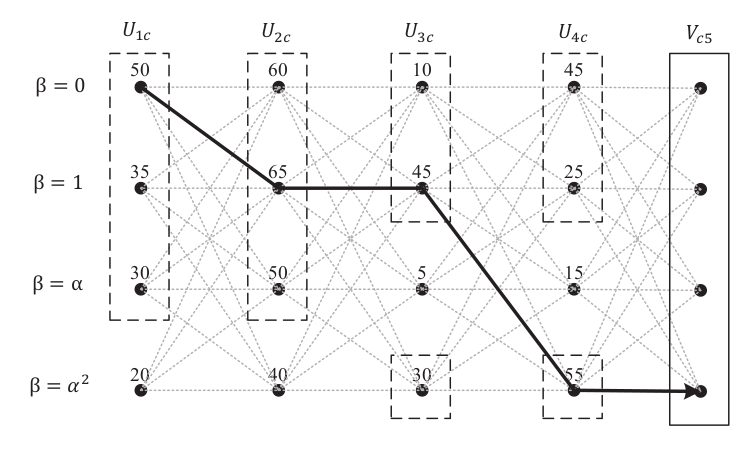
配置集

尽管前文说到配置集只在每个变量节点最大的 \(n_{max}\) 中选取，但是实际上，为了保证能够对每个符号都能得到至少一个配置集，就需要在这种 真正的 配置集之外，再补充一个集合。 这一集合，限制 除了一个变量节点可以随意选外，其它每个变量节点都必须选其最大值。也就是说，这个集合拥有\((d-1) * (q-1) + 1\)个，其中 \(d-1\) 是指涉及的变量节点为当前校验节点度数减去当前变量节点，\(q-1\)是自由选取的变量节点可选的符号范围，\(+1\) 是要补充 重复计算的 每个变量节点都选最大值的情况。

T-EMS

T-EMS 相对于 EMS，缩小了配置集，解长码时更有优势。

首先需要将 LLR 差分化，即套用如下公式：

\[\Delta U_{p c}\left[\eta_{p}=x+\beta_{p}^{(1)}\right]=U_{p c}\left[\beta_{p}^{(1)}\right]-U_{p c}[x], \quad x \in G F(q)\]

其中，\(\beta_p^{(1)}\) 表示变量节点中最可信（最大）的 LLR 的下标。注意，赋值对象的下标为 \(\eta_{p}=x+\beta_{p}^{(1)}\)。

以上图中 \(U_2\) 为例，\(\beta_p^{(1)}=1\)，\(U_2[0]=U[1]-U[1]=65-65=0\)，\(U_2[1]=U[1]-U[0]=65-60=5\)，\(U_2[\alpha]=U[1]-U[\alpha^2]=65-40=25\)，便得到下图。

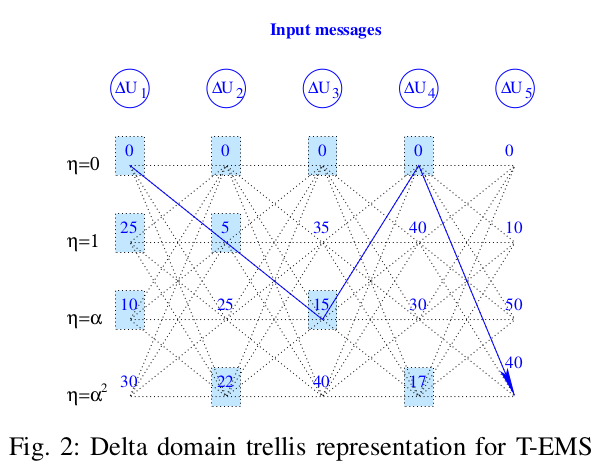
由于是与最可信的做减法，因此差分后的值越小就越可信。那么目前最可信的就是第一行。

我们在每行（除第一行外）中选取最小的 \(n_r\) 个，就构成了 TEMS 的配置集，也就是上图中蓝框的 10 个。 TEMS 的配置集中有 \(d_c-1+n_r(q-1)=10\) 个

然后类似地选取配置集中总和最小的，求出对应 VN 的 GF 上的值。不过此时的 GF 还需要逆差分：

\[V_{c p}\left[\beta=\eta-\beta_{\max }+\beta_{p}^{(0)}\right]=-\Delta V_{c p}[\eta], \eta \in \mathrm{GF}(q), p=1 \cdots d_{c}\]

分块 LDPC

\(z_f\)：分块大小，又称 lifting size

ratio：\(z_f/n_b\)

  • \(n_6\)：重量为 6 的列数（基矩阵）
  • \(n_2\)：一般为 m-1，因为矩阵最右一般是 m-1 x m 的双对角矩阵，且列重为 2 的列越少越好

圈四：基矩阵中有一块 2x2 的部分都非 -1

打孔： - 不传输，故收到的似然比直接置为 0（y = 0 or 1 等概） - 码率要把打孔的去掉 - 打孔的列一般都是列重很高，因为译码时极易恢复

SC-LDPC

空间耦合 LDPC

#学习
Licensed under CC BY-NC-SA 4.0